Numbers serve as the building blocks of mathematics and its theories. While familiar number systems like the integers, rational numbers, real numbers, and complex numbers dominate everyday calculations, there exist more obscure number systems that unveil profound insights and applications in various areas of mathematical analysis (and maybe allow breakthroughs in other fields too!). Three such uncommon number systems are the p-adic numbers, quaternions, and transfinite numbers.
p-adic Numbers: An Opposite approach to Infinite Digits
The p-adic numbers provide an alternative perspective on numbers and their relationships by altering the concept of infinite digits. The "p" stands for prime. We all are familiar with the fact that any number can be represented with infinite decimal digits going to the right.
3 = 3.000000000....
But can't infinite digits go to the left as well?
3 = ...0000000003
Suddenly, by shifting the side we have infinite digits for, we have gone from real numbers to p-adic numbers! Why is this so useful? Well, think about it. When we are working with huge numbers like 2⁹⁹⁹⁹⁹⁹ then it is not possible to show every digit of the number. Hence, we can represent them in p-adic form that simplifies the representation significantly. Just to make you curious: in p-adic numbers, the following holds true.
82 is much closer to 1 than 81 in 3-adic number system.
p-adic numbers have found applications in various fields, including number theory and mathematical physics. They have played a significant role in solving Diophantine algebra, which are polynomial equations with integer coefficients that seek integer solutions.
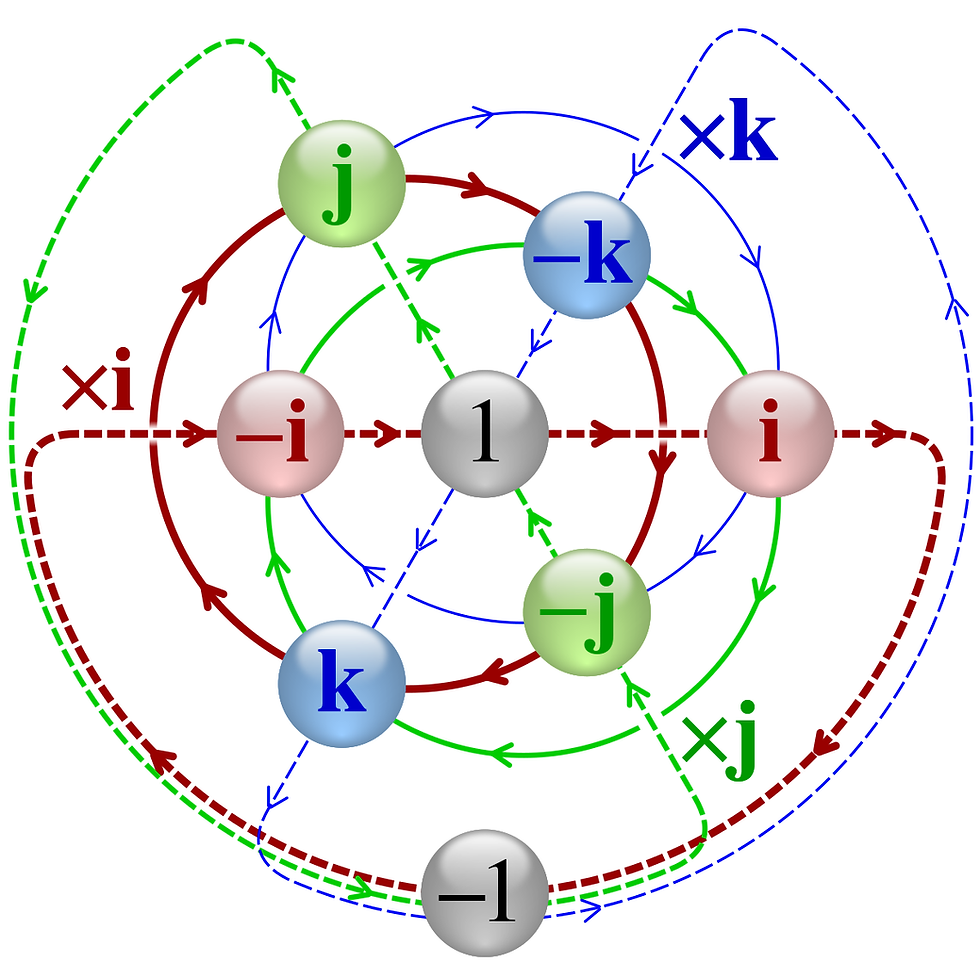
Quaternions: Extending the Imaginary Components
For understanding this, learning about complex numbers might be a better start to this section. Nonetheless, it is important to recall that:
i² = -1
After grasping this idea, consider this now:
i² = j² = k² = -1
BUT
i ≠ j ≠ k
These kinds of number systems do not follow typical properties like commutativity of multiplication (a * b = b * a). Such innovative definitions and premises can have mind-boggling implications of ease and complexity both. Quaternions find applications in quantum physics most prominently. It can help simplify the processes of calculating spin and rotation! Mainly, quaternions can help represent rotation in multiple kinds of axes in an easier manner.
Transfinite Numbers: Beyond the Infinite
Transfinite numbers challenge our intuitive understanding of infinity. Introduced by mathematician Georg Cantor in the late 19th century, transfinite numbers are a way of comparing and describing different sizes of infinity. Cantor's groundbreaking work revealed that not all infinities are equal; some are "larger" than others. These transfinite numbers are typically "larger than any finite numbers"
Cantor's concept of transfinite numbers revolves around sets and their cardinalities (sizes). He introduced the idea of aleph numbers (ℵ₀, ℵ₁, ℵ₂, etc.), where ℵ₀ represents the cardinality of the set of natural numbers (countable infinity), and larger alephs represent higher infinities. The continuum hypothesis, a famous conjecture in set theory, addresses the relationship between ℵ₁ and the cardinality of the real numbers, delving into the complexity of different infinities. There are various kinds of sizes of infinity and the difference between real and integer number sets' cardinalities.
Transfinite numbers have implications in set theory, logic, and the foundations of mathematics. Cantor's work sparked debates about the nature of infinity and led to the development of axiomatic set theory, which serves as the framework for modern mathematics. This number system fills in a hole critical to modern mathematical theory.
Connecting the Uncommon Threads
Though seemingly disparate, these uncommon number systems share a common theme of challenging conventional notions. They push the boundaries of mathematical imagination and invite exploration beyond the well-trodden paths of arithmetic.
Moreover, these number systems often find unexpected connections. For instance, p-adic numbers have been linked to the study of modular forms and their role in number theory, whereas quaternions have connections to the geometry of rotations. Transfinite numbers touch on philosophical debates about the nature of the infinite and the foundations of mathematical thought.
In conclusion, numbers serve as remarkable examples of how mathematical creativity can lead to unconventional and profound concepts beyond the typical integers and real numbers. While these number systems might not be encountered in everyday calculations, their influence on various branches of mathematics and their applications in physics and computer science underscore their significance. By embracing these unconventional number systems, mathematicians and researchers continue to expand the horizons of mathematical exploration and understanding. As an interested reader, these number systems can build critical thinking skills to comprehend rules of the new systems and try to use them from time to time.
Bibliography
Houston-Edwards, Kelsey. “An Infinite Universe of Number Systems.” Quanta Magazine, 19 Oct. 2020, www.quantamagazine.org/how-the-towering-p-adic-numbers-work-20201019/.
O’Connor, J. J., and E. F. Robertson. “Georg Cantor - Biography.” Maths History, Oct. 1998, mathshistory.st-andrews.ac.uk/Biographies/Cantor/.
Rowland, Eric. “1 Billion Is Tiny in an Alternate Universe: Introduction to P-Adic Numbers.” YouTube, 5 Aug. 2022, www.youtube.com/watch?v=3gyHKCDq1YA.
コメント