
Making predictions is easy... because it is just so ambiguous.
"There is a high probability of rainfall tomorrow" is quite ambiguous, but probably signifies that it rains more times than it doesn't.
"70% probability of rainfall tomorrow" means if you were omnipotent and could replay tomorrow 10 times, 7 times would face rainfall but 3 would not.
"Brier Score of 0.2 for a 70% probability of rainfall tomorrow"... Now, what does that mean? Who is a "Brier"?
Forecasting is the practice of mathematical prophesying. That's right, prophesying: the voodoo "I can predict the future" kind. The role of mathematics, as you may guess, is the contribution of probabilities. Forecasters analyse and meta-analyse multiple events to then use their best judgement and give a probability, a guess, a forecast. Maybe, if you learn this craft, you could start becoming eerily good at meaningful forecasts? The things that matter: diseases, elections, recessions, etc. This is why forecasting has far-reaching applications from medicine to economics, so why not learn a few basics?
Problem with Words
Going back about 80 years, we can come acorss the first instance of words being uselessly confusing in forecasts. So much so that "80-20" odds were confused to be the same as "20-80" odds! Well, here is the story:
It is the late 1940s and Yugoslavia has just seceded from the Soviet Union spreading a fear of looming war. Just a couple years late, in March 1951, United States's National Intelligence Estimate is released stating: "we believe that the extent of [Eastern European] military and propaganda preparations indicates that an attack on Yugoslavia in 1951 should be considered a serious possibility". A "serious possibility" sounds pretty straightforward and direct, right? What would it mean: probably around 70%, maybe even 80%? Think again.
Sherman Kent, a legend in CIA and intelligence analysis, wondered too. He, personally, thought the words signified a "65-35" odds in favour of an attack. What confused him was a senior State Department official assumed the odds were much lower when he had read "serious possibility". Confused, he went to his team where one statistician said he thought the "serious possibility" signified 80-20 odds, while another team member thought it represented 20-80 odds, the complete opposite!
This was obviously no good. A team of expert statisticians could not just agree on a phrase with two complete opposite odds in their minds. Forecasting needed an update.
Brier Score
So, how do we mathematicise our forecasts? Let's add probabilities. There is no longer a "serious possibility" of it raining, there is a "70%" probability. But then do you trust such a probability? How can we trust a national intelligence agency more than a random bugger off the street? Probably because they have more credibility. But how much more credibility? Can we quantify it?
We can. But first, we need more data. Over time, as you make more and more predictions with precise "probabilities" of your own success, you allow a Brier Score to be calculated.
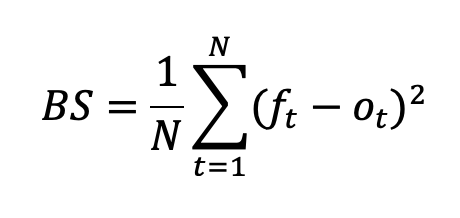
The Brier Score is basically a mean squared error algorithm. It was proposed by Glenn Brier and tells you the reliability of someone's prediction. In its rawest form, the formula is as above, but that makes it look a lot more complicated than it is. Actually, why not take a real world example for better understanding.
What even is that formula?
The formula is quite simple when I colour-code it. Mathematicians like making things look more complicated.

This is just finding the difference in actual and predicted value.
This finds the square of these differences.
This finds the mean value of all the squares
All in all, giving the mean squared error.
Step 1: Background
Alex is a Chennai Super Kings (CSK) fan in the Indian Premier League, and he refuses to believe any team can outplay it. He thinks CSK will win every match with a 100% probability.
Brian is a CSK fan, but is less emotional and believes in previous statistics. He looks at all the head-to-head of CSK against the opponent in previous IPLs to determine the likelihood of winning.
Charlie is a CSK hater, and he refuses to believe CSK could beat any other team in the IPL. He thinks CSK will win every match with a 0% probability.
Step 2: Probabilities
Here are their pre-game estimates for all the five matches so far.
Alex | Brian | Charlie |
100% CSK beats RCB | 65% CSK beats RCB | 0% CSK beats RCB |
100% CSK beats GT | 40% CSK beats GT | 0% CSK beats GT |
100% CSK beats DC | 66% CSK beats DC | 0% CSK beats DC |
100% CSK beats SRH | 75% CSK beats SRH | 0% CSK beats SRH |
100% CSK beats KKR | 63% CSK beats KKR | 0% CSK beats KKR |
Great, now obviously CSK did not win all matches, but at the same time, they won a majority. Since Alex kept predicting a 100% certainty, did he predict better or did the safer predictions of Brian fare better? Maybe the pessimist Charlie beat them both? How do we judge their credibility? Remember... Brier Scores!
Step 3: Brier Score!
CSK, in actuality, beat RCB, GT, and KKR. Let us encode a win to be a value of "1", and a loss to be a value of "0". We have now reached the territory of Brier Scores. Nothing to be spooked about though, it is just a three stage process: error, square, mean. We can calculate the difference in each predicted forecast and actual outcome as the error. We can square the error term. We can then find the mean result, giving us the mean squared error.
Alex | Brian | Charlie |
(1.00 - 1)² = 0 | (0.65 - 1)² = 0.1225 | (0.00 - 1)² = 1 |
(1.00 - 1)² = 0 | (0.40 - 1)² = 0.36 | (0.00 - 1)² = 1 |
(1.00 - 0)² = 1 | (0.66 - 0)² = 0.4356 | (0.00 - 0)² = 0 |
(1.00 - 0)² = 1 | (0.75 - 0)² = 0.5625 | (0.00 - 0)² = 0 |
(1.00 - 1)² = 0 | (0.63 - 1)² = 0.1369 | (0.00 - 1)² = 1 |
Mean = 2/5 = 0.4 | Mean = 1.6175/5 = 0.32 | Mean = 3/5 = 0.6 |
These mean values are the infamous Brier Scores. Just to note, the lower your Brier score, the better you are at predictions. This is the second layer of forecasting. Now, the next forecast made by these individuals can be attached with their brier score to show just how reliable they are. The lower your score the more reliable you are! The higher your score, and you are probably making mindless comments.
Charlie, with a high and unreliable Brier score of 0.6, says CSK has a 0% chance of beating Mumbai Indians the next match (sounds unlikely). Alex, with a reasonable yet average score of 0.4, says CSK has a 100% chance of beating MI the next match (maybe I am secretly Alex?). And our forecasting champion, with his calculative predictions and a stronger score of 0.32, claims CSK has a 44.4% chance of beating MI the next match (okay, are we sure the Brier Score is reliable? MI having a higher chance of beating CSK? Let's see...)
Conclusion
Maybe this has gotten you charged up to test your own skills. Get together with your friends and see who can predict the next IPL matches correctly... Maybe, even predict one of the many state elections! Subsequently, calculate the Brier Scores for each prediction and determine the forecasting champion. Remember, the journey of forecasting is an iterative process focused on continuous learning and refinement. The more you refine, the better your predictions, and the more reliable you are. Maybe next time, you ought to trust your friend with the lower Brier score when making a forecast!
Bibliography and Suggested Further Reading
Brier, Glenn W. “Verification of Forecasts Expressed in Terms of Probability.” Wayback Machine, Jan. 1950, web.archive.org/web/20171023012737/docs.lib.noaa.gov/rescue/mwr/078/mwr-078-01-0001.pdf. Archived on Wayback Machine from original https://docs.lib.noaa.gov/rescue/mwr/078/mwr-078-01-0001.pdf.
Lowe, David. “Brier Scores.” Scrum & Kanban, 13 June 2016, scrumandkanban.co.uk/brier-scores/. Accessed 11 Apr. 2024.
myKhel. “IPL Head to Head Records.” MyKhel, 2024, www.mykhel.com/cricket/ipl-head-to-head-records-s4/.
Tetlock, Philip. Superforecasting. (Export Edition). Random House, 2016.
Comentarii